The work with the Polymath project was published on Research in the Mathematical Sciences.
Here is the list of Polymath8b authors (arranged in alphabetical order of surname): Ignace Bogaert, Aubrey de Grey, Gergely Harcos, Emmanuel Kowalski, Philippe Michel, James Maynard, Paul Nelson, Pace Nielsen, Eytan Paldi, Andrew V. Sutherland, Terence Tao, Xiao-Feng Xie
Abstract: For any  , let
, let 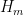 denote the quantity
denote the quantity 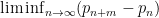 , where
, where  is the
is the 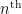 prime. A celebrated recent result of Zhang showed the finiteness of
prime. A celebrated recent result of Zhang showed the finiteness of 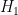 , with the explicit bound
, with the explicit bound 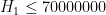 . This was then improved by us (the Polymath8 project) to
. This was then improved by us (the Polymath8 project) to  , and then by Maynard to
, and then by Maynard to  , who also established for the first time a finiteness result for
, who also established for the first time a finiteness result for 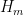 for
for 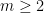 , and specifically that
, and specifically that 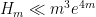 . If one also assumes the Elliott-Halberstam conjecture, Maynard obtained the bound
. If one also assumes the Elliott-Halberstam conjecture, Maynard obtained the bound 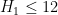 , improving upon the previous bound
, improving upon the previous bound 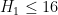 of Goldston, Pintz, and Y{\i}ld{\i}r{\i}m, as well as the bound
of Goldston, Pintz, and Y{\i}ld{\i}r{\i}m, as well as the bound 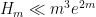 . In this paper, we extend the methods of Maynard by generalizing the Selberg sieve further, and by performing more extensive numerical calculations. As a consequence, we can obtain the bound
. In this paper, we extend the methods of Maynard by generalizing the Selberg sieve further, and by performing more extensive numerical calculations. As a consequence, we can obtain the bound  unconditionally, and
unconditionally, and  under the assumption of the generalized Elliott-Halberstam conjecture. Indeed, under the latter conjecture we show the stronger statement that for any admissible triple
under the assumption of the generalized Elliott-Halberstam conjecture. Indeed, under the latter conjecture we show the stronger statement that for any admissible triple  , there are infinitely many
, there are infinitely many  for which at least two of
for which at least two of 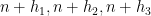 are prime, and also obtain a related disjunction asserting that either the twin prime conjecture holds, or the even Goldbach conjecture is asymptotically true if one allows an additive error of at most
are prime, and also obtain a related disjunction asserting that either the twin prime conjecture holds, or the even Goldbach conjecture is asymptotically true if one allows an additive error of at most 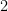 , or both. We also modify the “parity problem” argument of Selberg to show that the
, or both. We also modify the “parity problem” argument of Selberg to show that the  bound is the best possible that one can obtain from purely sieve-theoretic considerations. For larger
bound is the best possible that one can obtain from purely sieve-theoretic considerations. For larger 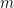 , we use the distributional results obtained previously by our project to obtain the unconditional asymptotic bound
, we use the distributional results obtained previously by our project to obtain the unconditional asymptotic bound 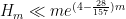 , or
, or 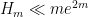 under the assumption of the Elliott-Halberstam conjecture. We also obtain explicit upper bounds for
under the assumption of the Elliott-Halberstam conjecture. We also obtain explicit upper bounds for 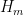 when
when 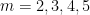 .
.
 The Polymath8 participants was featured on the June/July cover of Notices of the American Mathematical Society, the world’s most widely read mathematical journal.
The Polymath8 participants was featured on the June/July cover of Notices of the American Mathematical Society, the world’s most widely read mathematical journal.
 …
… This problem is to solve the Magic Square Problem (constrained and unconstrained versions), a combinatorial optimization problem, using
This problem is to solve the Magic Square Problem (constrained and unconstrained versions), a combinatorial optimization problem, using