Projects

September 10, 2018
0

Work on Big Data Analytics and Urban Computing

I have worked on big data analytics for different transportation-related topics. Here is a list of publications in this field.

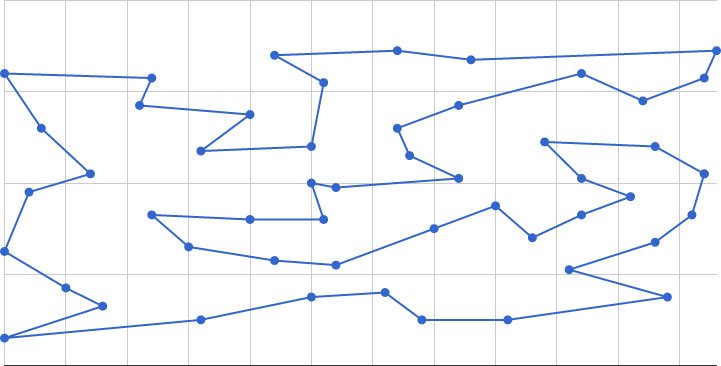
Xiao-Feng Xie and Zun-Jing Wang. Examining travel patterns and characteristics in a bikesharing network and implications for data-driven decision supports: Case study in the Washington DC area. Journal of Transport Geography, 71: 84-102, 2018.

@Article{Xie2018Bike,
Title = {Examining travel patterns and characteristics in a bikesharing network and implications for data-driven decision supports: Case study in the {Washington DC} area},
Author = {Xiao-Feng Xie and Zun-Jing Wang},
Journal = {Journal of Transport Geography},
Volume = {71},
Pages = {84--102},
PDF={http://www.wiomax.com/team/xie/paper/JTRG18Pre.pdf},
Doi = {10.1016/j.jtrangeo.2018.07.010},
Year = {2018}
}

Xiao-Feng Xie and Zun-Jing Wang. Multiscale crash analysis: A case study of integrating FARS, Maryland’s crash data, and Montgomery County’s traffic violation data. In Transportation Research Board (TRB) Annual Meeting, number 18-2283, Washington, DC, 2018.

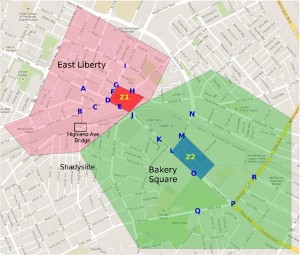
@InProceedings{xie2018multiscale,
title={Multiscale crash analysis: A case study of integrating {FARS}, {Maryland}'s crash data, and {Montgomery County}'s traffic violation data},
author={Xie, Xiao-Feng and Wang, Zun-Jing},
Booktitle = {Transportation Research Board (TRB) Annual Meeting},
number={18-2283},
Address = {Washington, DC},
LNK={https://trid.trb.org/View/1495254},
PDF={http://www.wiomax.com/team/xie/paper/TRB18.pdf},
year={2018}
}

Yiming Gu, Zhen Qian, and Xiao-Feng Xie. An unsupervised learning approach for analyzing traffic impacts under arterial road closures: Case study of East Liberty in Pittsburgh. Journal of Transportation Engineering, 142(9): 4016033, 2016.

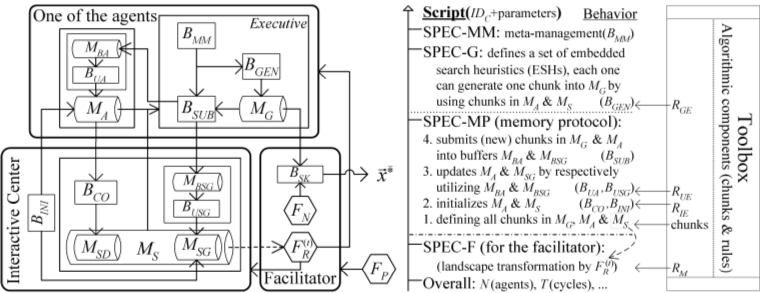
@Article{Gu2016,
Title = {An unsupervised learning approach for analyzing traffic impacts under arterial road closures: Case study of {East Liberty} in {Pittsburgh}},
Author = {Yiming Gu and Zhen Qian and Xiao-Feng Xie},
journal = {Journal of Transportation Engineering},
Year = {2016},
Number = {9},
Volume = {142},
Pages = {04016033},
Doi={10.1061/(ASCE)TE.1943-5436.0000860},
publisher={American Society of Civil Engineers}
}

Xiao-Feng Xie and Zun-Jing Wang. An empirical study of combining participatory and physical sensing to better understand and improve urban mobility networks. In Transportation Research Board (TRB) Annual Meeting, number 3238, Washington, DC, 2015.

@InProceedings{Xie2015,
Title = {An empirical study of combining participatory and physical sensing to better understand and improve urban mobility networks},
Author = {Xiao-Feng Xie and Zun-Jing Wang},
Booktitle = {{Transportation Research Board (TRB) Annual Meeting}},
number={3238},
PDF={http://www.wiomax.com/team/xie/paper/TRB15LBSN.pdf},
PPT={http://www.wiomax.com/team/xie/demo/TRB15_demo_BigData_UrbanInformatics.pdf},
LNK={https://trid.trb.org/View/1337999},
Year = {2015},
Address = {Washington, DC}
}

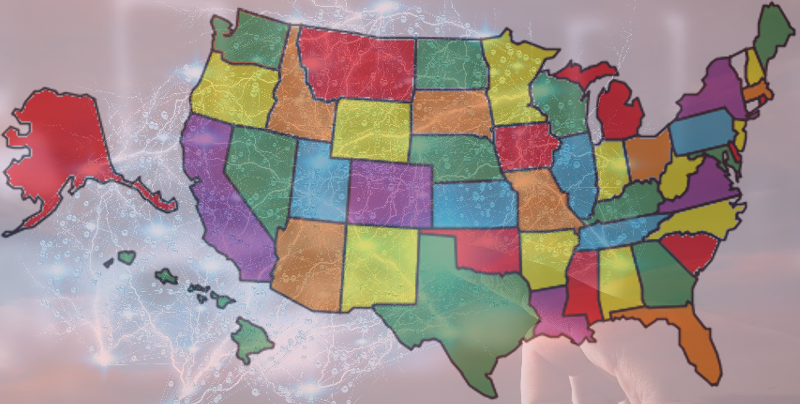
X. Xie and Z. J. Wang, “Uncovering Urban Mobility and City Dynamics from Large-Scale Taxi Origin-Destination (O-D) Trips: Case Study in Washington DC Area,” WIOMAX, WIO-TR-18-003, 2018.

@TechReport{xie2018uncovering,
title = {Uncovering Urban Mobility and City Dynamics from Large-Scale Taxi Origin-Destination ({O-D}) Trips: Case Study in {Washington DC} Area},
author = {Xiao-Feng Xie and Wang, Zunjing Jenipher},
year = {2018},
number = {WIO-TR-18-003},
Institution={WIOMAX},
PDF = {http://www.wiomax.com/doc/report/WIO-TR-18-003.pdf},
DOI = {10.13140/RG.2.2.32170.72644},
urldate = {2018-07-25},
upddate = {2018-07-25}
}

February 15, 2018
0

(Constrained) Numerical Optimization Problem (NOP)

Category : Code

A general constrained numerical optimization problem (NOP) may be written as follows:

$\begin{array}{rcll} \min &~& f(\mathbf{x}) & \\ \mathrm{subject~to} &~& g_i(\mathbf{x}) =\in [c_i, d_i] &\text{for } i=1,\ldots,n \end{array}$

where $f(\mathbf{x})$ is the objective function and each $g(\mathbf{x})$ is a constraint function to be satisfied, and $c$ and $d$ are constants. Each function can be nonlinear and non-smooth. If there is no constraint (i.e., $n=0$ ), then the problem becomes an unconstrained optimization problem.

NOP Instance Implementation [in DEPSO or SCO]

To implement your own problem instance, you need create a JAVA source file, normally placed in the directory problem/unconstrained (if the problem has no constraint) or problem/constrained (if the problem has constraints).

Implementation Tips: 1) all the variable bounds must be specified; 2) any equality constraint should be relaxed by a small tolerance value (e.g., ε=1E-4 for problem.constrained.Michalewicz_G3); and 3) problem.ProblemEncoder and problem.UnconstrainedProblemEncoder are the parental classes of all constrained (e.g., problem.constrained.Michalewicz_G1) and unconstrained (e.g., problem.unconstrained.GoldsteinPrice) problems, respectively.

We use Michalewicz’s G1 problem as an example to explain the steps to implement an instance in JAVA. Here is the mathematical form:

There are detailed comments in src/problem/constrained/Michalewicz_G1.java. It should be easy to figure out the implementation details.

Compiling Tips: Type “ant” to build, and the output file will be dist/depso.jar. You can also import the project into Eclipse IDE.

Testing Tips: There is a tool to calculate the output responses of the problem based on the input values. The tool has a main class problem.Simulator. It has two parameters, one is the function, and the second is the input values (separated by “,”). An example is:

$ java -cp dist/depso.jar problem.Simulator problem.constrained.Michalewicz_G1 "1,1,1,1,1,1,1,1,1,3,3,3,1"

December 23, 2017
0

MAOS-TSP: Project Portal

Tags : code optimization software

Category : Open Source

MAOS-TSP [1] is a multiagent optimization system (MAOS) for solving the Traveling Salesman Problem (TSP).

Related Information: Please find other related code and software in our Source Code Library.

Basic Description	What’s New	Directories & Files	Command Line & Parameters	Output Information	References	Contact

CkyUNmzUYAAdZOV

License Information: You can redistribute and/or modify it under the terms of the Creative Commons Non-Commercial License 3.0.

System Requirements: MAOS-TSP is a platform-independent software developed by JAVA version 1.5 or above.

What’s New

Version V1.0.004 [Download | github]:

– Add a parameter “opt=[length]” to use the length of the shortest tour as another stopping criterion. (Based on the request by J. Bossek)

Version V1.0.003:

– Solver “STD_PRB_3Opt_2L_REAX+SEAX_1J”: 1) Two-level representation for 3-opt: reduce the time complexity of Tour Segment Inversion from O(n) to O(sqrt(n)); 2) Locking common edges during the sub-cycles bridging process in the generalized EAX; 3) Sorting in k Nearest Neighbors: reduce the time complexity from O(nlog(n)) to O(n+klog(k)).

Version V1.0.002:

– Solver “STD_PRB_3Opt_REAX+SEAX”: It implements the solver for original MAOS-TSP algorithm [1]. This solver has shown to be competitive in solving middle-scale TSP instances (1000 – 6000 nodes) as comparing to some state-of-the-art algorithms, without using explicit local search (e.g. LK variants) during the runtime cycles.

For example, it found the best-so-far solution (located in myprojects/tasks/TSP/solution) for the open instance fdp3256 in the VLSI Data Sets.

– Setting parameters: TSP:Problem, N, T, Tcon, Solver.

Directories & Files

binary	                           // the binary code of MAOS-TSP
source                             // the source code of MAOS-TSP
myprojects                         // user directory
|-----> examples.bat               // commandline examples
|-----> results                    // the directory for storing runtime results
|-----> setting                    // the setting directory  
	|-----> kernel             // the setting directory for MAOS Kernel
	|-----> TSP                // the setting directory for TSP solvers
                |-----> solver     // the directory containing solver script files (the name of each file is Solver_Name)
                                   // Examples: "STD_PRB_3Opt_REAX+SEAX" and "STD_PRB_3Opt_2L_REAX+SEAX_1J"
|-----> tasks                      // task directory
        |-----> TSP
                |-----> instance   // GCP instances of the TSPLIB format (Problem_Name with the default suffix .tsp) 
                                   // Example: rl1323.tsp (Problem_Name is rl1323)
                |-----> solution   // the directory for storing solutions of TSP instances
                                   // For a normal solution, the file name is Problem_Name.(objective value).tour
                                   // If objective value is removed from the file name, the solution is considered as optimal.
                                   // Example: fdp3256.tour

// Typical benchmark instances can be found in the TSPLIB and VLSI data sets.

Command Line & Parameters

MAOS-TSP is executed on the command line (Enter the directory “myprojects”, and execute maosKernel.MAOSExecuter). Here is a typical example (See the file “myprojects/Examples.bat” for more examples), in which a user should specify JAVA options, general parameters, problem instance, and solver instance:

$ cd myprojects
$ java -server -Xmx512M -cp ../binary/MAOS_SEQ.jar maosKernel.MAOSExecuter TSP:Problem=rl1323 N=300 T=500 Tcon=100 DUP_TIMES=5 solver=STD_PRB_3Opt_2L_REAX+SEAX_1J

//java: the JAVA executor, JAVA Runtime Environment Version 1.5 or above is preferred
//maosKernel.MAOSExecuter: the main execution entrance of the MAOS program

JAVA Options (See “java -help” for more information):

There are two recommended optional parameters for java:
  -server: select the "server" VM, which is normally faster than the "client" VM
  -Xmx: set maximum Java heap size. Using a large enough size may prevent from the "out of memory" error

Moreover, the "-cp" option is used for loading the binary file "../binary/MAOS_SEQ.jar".

General Parameters:

NAME         VALUE_type   Range      Default_Value   Description

TSP:Problem  String      *	     <Problem_Name>  The problem instance to be solved
--------------------------------------------------------------------------------------------------
N            integer     >1          300 	     The number of agents
T            integer     >0          500	     Terminate condition: The maximum learning cycles
Tcon         integer     >0          100             Terminate condition: The number of cycles as the best state is unvaried

DUP_TIMES    integer     >0          10		     Number of trials
--------------------------------------------------------------------------------------------------
Solver       String      *	     <Solver_Name>   The name of the script of the actual solver
--------------------------------------------------------------------------------------------------
opt          integer    >0           None            The lower bound tour length for termination

//The explanation of Problem_Name and Solver_Name can be found in Directories & Files.

Output Information

For the output, we provide screen output, output a file for the running result, and stored the best solution ever found.

Screen Output:

[Initialization information]: provide the parsing information during the initialization.
[Runtime information]: The program outputs runtime information, i.e., the current best evaluation values, execution time, at every "Tout" cycles.
[Summary information]: At the end, it outputs the input variables, response values, and evaluation values <Vcon, Vopt> of the best solution.

Result File:

The result file will be stored at the directory "myprojects/results".

Solution File:

The best solution (better than any previous solutions) will be stored at the directory "myprojects/tasks/TSP/solution" (of the TSPLIB format).

References

[1] Xiao-Feng Xie and Jiming Liu. Multiagent optimization system for solving the traveling salesman problem (TSP). IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 39(2): 489-502, 2009.

@Article{xie2009multiagent,
Title = {Multiagent optimization system for solving the traveling salesman problem ({TSP})},
Author = {Xiao-Feng Xie and Jiming Liu},
Journal = {IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics},
Year = {2009},
Number = {2},
Pages = {489--502},
PDF={http://www.wiomax.com/team/xie/paper/TSMCB09.pdf},
DOI={10.1109/TSMCB.2008.2006910},
Code={http://www.wiomax.com/maos-tsp},
Volume = {39}
}

November 22, 2017
0

MAOS-GCP: Project Portal

Tags : code optimization software

Category : Software

MAOS-GCP [1] is a multiagent optimization system (MAOS) for solving the Graph Coloring Problem (GCP).

Related Information: MAOS-GCP shares the MAOS kernel with other MAOS applications (e.g. MAOS-TSP, MAOS-FSP, MAOS-QAP, MAOS-QKP), and contains some modules that are specifically for tacking GCP. Please find other related code and software in our Source Code Library.

Basic Description	What’s New	Directories & Files	Command Line & Parameters	Output Information	References

License information: MAOS-GCP is free software; you can redistribute it and/or modify it under the Creative Commons Non-Commercial License 3.0.

System Requirements: MAOS-GCP is a platform-independent software developed by JAVA version 1.5 or above.

What’s New

Version: V1.0.001 [Download | Github]:

Solver “DS_GGBX_STD_QT”: It implements the original MAOS-GCP algorithm [1]. Based on the MAOS framework, the Quasi-Tabu local search rule and the grouping-based recombination search rule are used for tackling neutrality and ruggedness in the GCP landscape, respectively.

Setting parameters: GCP:Problem, N, T, Tcon, Solver.

Directories & Files

binary	                           // the binary code of MAOS-GCP
source                             // the source code of MAOS-GCP
myprojects                         // user directory
|-----> examples.bat               // commandline examples
|-----> results                    // the directory for storing runtime results
|-----> setting                    // the setting directory  
	|-----> kernel             // the setting directory for MAOS Kernel
	|-----> GCP                // the setting directory for GCP solvers
                |-----> solver     // the directory containing solver script files (the name of each file is Solver_Name)
                                   // Examples: "DS_GGBX_STD_QT"  (Solver_Name is DS_GGBX_STD_QT)
|-----> tasks                      // task directory
        |-----> GCP
                |-----> instance   // GCP instances of the DIMACS standard format (Problem_Name with the default suffix .col) 
                                   // Example: le450_15c.col (Problem_Name is le450_15c)
                |-----> solution   // the directory for storing solutions of GCP instances
                                   // For a normal solution, the file name is Problem_Name_k(KColor).(objective value).sln
                                   // If objective value is removed from the file name, the solution is considered as optimal.
                                   // Example: le450_15c_k15.sln (Problem_Name=le450_15c, KColor=15)

// Typical benchmark instances can be found from here (Note that each .b file of the compressed format should be translated by binformat.shar).

Command Line & Parameters

MAOS-GCP is executed on the command line (Enter the directory “myprojects”, and execute maosKernel.MAOSExecuter). Here is a typical example (See the file “myprojects/Examples.bat” for more examples), in which a user should specify JAVA options, general parameters, problem instance, and solver instance:

$ cd myprojects
$ java -server -cp ../binary/MAOS_INT.jar maosKernel.MAOSExecuter GCP:problem=le450_15c,kColor=15 N=25 T=50 solver=DS_GGBX_STD_QT

//java: the JAVA executor, JAVA Runtime Environment Version 1.5 or above is preferred
//maosKernel.MAOSExecuter: the main execution entrance of the MAOS program

JAVA Options (See “java -help” for more information):

There is one recommended optional parameter for java:
  -server: select the "server" VM, which is normally faster than the "client" VM

The "-cp" option is used for loading the binary file "../release/MAOS_INT.jar".

General Parameters:

NAME         VALUE_type   Range      Default_Value   Description

GCP:Problem  String      *	     <Problem_Name>  The problem instance to be solved
    KColor   integer     >1          *               The number of colors for the problem instance
--------------------------------------------------------------------------------------------------
N            integer     >1          100 	     The number of agents
T            integer     >0          500	     Terminate condition: The maximum learning cycles
Tcon         integer     >0          -1              Terminate condition: The number of cycles as the best state is unvaried
                                                     //If Tcon==-1, then Tcon=T

DUP_TIMES    integer     >0          10		     Number of trials
--------------------------------------------------------------------------------------------------
Solver       String      *	     <Solver_Name>   The name of the script of the actual solver

//The explanation of Problem_Name and Solver_Name can be found in Directories & Files.

Output Information

For the output, we provide screen output, output a file for the running result, and stored the best solution ever found.

Screen Output:

[Initialization information]: provide the parsing information during the initialization.
[Runtime information]: The program outputs runtime information, i.e., the current best evaluation values, execution time, at every "Tout" cycles.
[Summary information]: At the end, it outputs the input variables, response values, and evaluation values <Vcon, Vopt> of the best solution.

Result File:

The result file will be stored at the directory "myprojects/results".

Solution File:

The best solution (better than any previous solutions) will be stored at the directory "myprojects/tasks/GCP/solution".

References

[1] Xiao-Feng Xie and Jiming Liu. Graph coloring by multiagent fusion search. Journal of Combinatorial Optimization, 18(2): 99-123, 2009.

@Article{xie2009graph,
Title = {Graph coloring by multiagent fusion search},
Author = {Xiao-Feng Xie and Jiming Liu},
Journal = {Journal of Combinatorial Optimization},
Year = {2009},
Number = {2},
Pages = {99--123},
PDF={http://www.wiomax.com/team/xie/paper/JOCO09.pdf},
DOI={10.1007/s10878-008-9140-6},
Code={http://www.wiomax.com/maos-gcp},
Volume = {18}
}

September 27, 2017
0

MAOS-QKP: Project Portal

Tags : code optimization software

Category : Software

MAOS-QKP is a multiagent optimization system (MAOS) for solving the Quadratic Knapsack Problem (QKP).

Related Information: MAOS-QKP shares the MAOS kernel with other MAOS applications (e.g. Graph Coloring Problem (GCP) and Traveling Salesman Problem (TSP)). Please find other related code and software in our Source Code Library.

Basic Description	What’s New	Directories & Files	Command Line & Parameters	Output Information	References

License information: MAOS-QKP is free software; you can redistribute it and/or modify it under the Creative Commons Non-Commercial License 3.0.

System Requirements: MAOS-QKP is a platform-independent software developed by JAVA version 1.5 or above.

What’s New

Version: V1.0.001 [Download | Github]:

Solver “STD_NLDUX”: It implements the original MAOS-QKP algorithm [1].
Setting parameters: QKP:Problem, N, T, Tcon, Solver.

Directories & Files

binary	                           // the binary code of MAOS-QKP
source                             // the source code of MAOS-QKP
myprojects                         // user directory
|-----> examples.bat               // commandline examples
|-----> results                    // the directory for storing runtime results
|-----> setting                    // the setting directory  
	|-----> kernel             // the setting directory for MAOS Kernel
	|-----> QKP                // the setting directory for QKP solvers
                |-----> solver     // the directory containing solver script files (the name of each file is Solver_Name)
                                   // Example: STD_NLDUX (Solver_Name is STD_NLDUX)
|-----> tasks                      // task directory
        |-----> QKP
                |-----> instance   // QKP instances of the B&S format (Problem_Name with the default suffix .txt) 
                                   // Example: jeu_100_025_01.txt (Problem_Name is jeu_100_025_01)
                |-----> solution   // the directory for storing solutions of QKP instances
                                   // For a normal solution, the file name is Problem_Name.(objective value).sln
                                   // If objective value is removed from the file name, the solution is considered as optimal.
                                   // Example: jeu_100_025_01.sln

// For your convenience, here are the benchmark instances and their solutions used in [1].

Command Line & Parameters

MAOS-QKP is executed on the command line (Enter the directory “myprojects”, and execute maosKernel.MAOSExecuter). Here is a typical example (See the file “myprojects/Examples.bat” for more examples), in which a user should specify JAVA options, general parameters, problem instance, and solver instance:

$ cd myprojects
$ java -cp ../binary/MAOS_BIN.jar maosKernel.MAOSExecuter QKP:Problem=jeu_100_025_01 N=500 T=500 DUP_TIMES=10 solver=STD_NLDUX

//java: the JAVA executor, JAVA Runtime Environment Version 1.5 or above is preferred
//maosKernel.MAOSExecuter: the main execution entrance of the MAOS program

JAVA Options (See “java -help” for more information):

There is one recommended optional parameter for java:
  -server: select the "server" VM, which is normally faster than the "client" VM

The "-cp" option is used for loading the binary file "../release/MAOS_BIN.jar".

General Parameters:

NAME         VALUE_type   Range      Default_Value   Description

QKP:Problem  String      *	     <Problem_Name>  The problem instance to be solved
--------------------------------------------------------------------------------------------------
N            integer     >1          100 	     The number of agents
T            integer     >0          500	     Terminate condition: The maximum learning cycles
Tcon         integer     >0          -1              Terminate condition: The number of cycles as the best state is unvaried
                                                     //If Tcon==-1, then Tcon=T

DUP_TIMES    integer     >0          2		     Number of trials
--------------------------------------------------------------------------------------------------
Solver       String      *	     <Solver_Name>   The name of the script of the actual solver

//The explanation of Problem_Name and Solver_Name can be found in Directories & Files.

Output Information

For the output, we provide screen output, output a file for the running result, and stored the best solution ever found.

Screen Output:

[Initialization information]: provide the parsing information during the initialization.
[Runtime information]: The program outputs runtime information, i.e., the current best evaluation values, execution time, at every "Tout" cycles.
[Summary information]: At the end, it outputs the input variables, response values, and evaluation values <Vcon, Vopt> of the best solution.

Result File:

The result file will be stored at the directory "myprojects/results".

Solution File:

The best solution (better than any previous solutions) will be stored at the directory "myprojects/tasks/QKP/solution" (of the QKPLIB format).

References

[1] Xiao-Feng Xie and Jiming Liu. A mini-swarm for the quadratic knapsack problem. In IEEE Swarm Intelligence Symposium, pages 190-197, Honolulu, HI, USA, 2007.

@InProceedings{Xie:2007p190,
Title = {A mini-swarm for the quadratic knapsack problem},
Author = {Xiao-Feng Xie and Jiming Liu},
Year = {2007},
Pages = {190--197},
Address = {Honolulu, HI, USA},
PDF={http://www.wiomax.com/team/xie/paper/SIS07.pdf},
DOI={10.1109/SIS.2007.368045},
Code={http://www.wiomax.com/maos-qkp},
Booktitle = {IEEE Swarm Intelligence Symposium}
}

September 22, 2017
0

MAOS-FSP: Project Portal

Tags : code optimization software

Category : Software

MAOS-FSP [1] is a multiagent optimization system (MAOS) for solving the Flowshop Scheduling Problem (FSP). MAOS-FSP shares the MAOS kernel with other MAOS applications (e.g. MAOS-GCP and MAOS-TSP), and contains some modules that are specifically for tacking FSP.

Related Information: Please find other related code and software in our Source Code Library.

Basic Description	What’s New	Directories & Files	Command Line & Parameters	Output Information	References

License information: MAOS-FSP is free software; you can redistribute it and/or modify it under the Creative Commons Non-Commercial License 3.0.

System Requirements: MAOS-FSP is a platform-independent software developed by JAVA version 1.5 or above.

What’s New

Version V1.0.001 [Download | Github]:

Solver “STD_NLDUX”: It implements the original algorithm [1].
Setting parameters: FSP:Problem, N, T, Tcon, Solver.

Directories & Files

binary	                           // the binary code of MAOS-FSP
source                             // the source code of MAOS-FSP
myprojects                         // user directory
|-----> examples.bat               // commandline examples
|-----> results                    // the directory for storing runtime results
|-----> setting                    // the setting directory  
	|-----> kernel             // the setting directory for MAOS Kernel
	|-----> FSP                // the setting directory for FSP solvers
                |-----> solver     // the directory containing solver script files (the name of each file is Solver_Name)
|-----> tasks                      // task directory
        |-----> FSP
                |-----> instance   // FSP instances (Problem_Name with the default suffix .txt) 
                |-----> solution   // the directory for storing solutions of FSP instances
                                   // For a normal solution, the file name is Problem_Name.(objective value).sln
                                   // If objective value is removed from the file name, the solution is considered as optimal.

Command Line & Parameters

MAOS-FSP is executed on the command line (Enter the directory “myprojects”, and execute maosKernel.MAOSExecuter). Here is a typical example (See the file “myprojects/Examples.bat” for more examples), in which a user should specify JAVA options, general parameters, problem instance, and solver instance:

$ cd myprojects
$ java -cp ../binary/MAOS_BIN.jar maosKernel.MAOSExecuter FSP:Problem=jeu_100_025_01 N=500 T=500 DUP_TIMES=10 solver=STD_NLDUX

//java: the JAVA executor, JAVA Runtime Environment Version 1.5 or above is preferred
//maosKernel.MAOSExecuter: the main execution entrance of the MAOS program

JAVA Options (See “java -help” for more information):

There is one recommended optional parameter for java:
  -server: select the "server" VM, which is normally faster than the "client" VM

The "-cp" option is used for loading the binary file "../release/MAOS_BIN.jar".

General Parameters:

NAME         VALUE_type   Range      Default_Value   Description

FSP:Problem  String      *	     <Problem_Name>  The problem instance to be solved
--------------------------------------------------------------------------------------------------
N            integer     >1          100 	     The number of agents
T            integer     >0          500	     Terminate condition: The maximum learning cycles
Tcon         integer     >0          -1              Terminate condition: The number of cycles as the best state is unvaried
                                                     //If Tcon==-1, then Tcon=T

DUP_TIMES    integer     >0          2		     Number of trials
--------------------------------------------------------------------------------------------------
Solver       String      *	     <Solver_Name>   The name of the script of the actual solver

//The explanation of Problem_Name and Solver_Name can be found in Directories & Files.

Output Information

For the output, we provide screen output, output a file for the running result, and stored the best solution ever found.

Screen Output:

[Initialization information]: provide the parsing information during the initialization.
[Runtime information]: The program outputs runtime information, i.e., the current best evaluation values, execution time, at every "Tout" cycles.
[Summary information]: At the end, it outputs the input variables, response values, and evaluation values <Vcon, Vopt> of the best solution.

Result File:

The result file will be stored at the directory "myprojects/results".

Solution File:

The best solution (better than any previous solutions) will be stored at the directory "myprojects/tasks/FSP/solution" (of the FSPLIB format).

References

[1] Xiao-Feng Xie. Round-table group optimization for sequencing problems. International Journal of Applied Metaheuristic Computing, 3(4): 1-24, 2012.

@Article{Xie2012a,
Title = {Round-table group optimization for sequencing problems},
Author = {Xiao-Feng Xie},
Journal = {International Journal of Applied Metaheuristic Computing},
Year = {2012},
Number = {4},
Pages = {1-24},
PDF={http://www.wiomax.com/team/xie/paper/IJAMC12.pdf},
DOI={10.4018/jamc.2012100101},
Code={http://www.wiomax.com/maos-qap},
Volume = {3}
}

September 22, 2017
0

MAOS-QAP: Project Portal

Tags : code optimization software

Category : Software

MAOS-QAP [1] is a cooperative group optimization system (MAOS) for solving the Quadratic Assignment Problem (QAP).

Related Information: MAOS-QAP shares the MAOS kernel with other MAOS applications (e.g. MAOS-GCP and MAOS-TSP), and contains some modules that are specifically for tacking QAP. Please find other related code and software in our Source Code Library.

Basic Description	What’s New	Directories & Files	Command Line & Parameters	Output Information	References

License information: MAOS-QAP is free software; you can redistribute it and/or modify it under the Creative Commons Non-Commercial License 3.0.

System Requirements: MAOS-QAP is a platform-independent software developed by JAVA version 1.5 or above.

What’s New

Version V1.0.001 [Download | Github]:

Solver “STD_NLDUX”: It implements the original algorithm [1].
Setting parameters: QAP:Problem, N, T, Tcon, Solver.

Directories & Files

binary	                           // the binary code of MAOS-QAP
source                             // the source code of MAOS-QAP
myprojects                         // user directory
|-----> examples.bat               // commandline examples
|-----> results                    // the directory for storing runtime results
|-----> setting                    // the setting directory  
	|-----> kernel             // the setting directory for MAOS Kernel
	|-----> QAP                // the setting directory for QAP solvers
                |-----> solver     // the directory containing solver script files (the name of each file is Solver_Name)
|-----> tasks                      // task directory
        |-----> QAP
                |-----> instance   // QAP instances (Problem_Name with the default suffix .txt) 
                |-----> solution   // the directory for storing solutions of QAP instances
                                   // For a normal solution, the file name is Problem_Name.(objective value).sln
                                   // If objective value is removed from the file name, the solution is considered as optimal.

Command Line & Parameters

MAOS-QAP is executed on the command line (Enter the directory “myprojects”, and execute maosKernel.MAOSExecuter). Here is a typical example (See the file “myprojects/Examples.bat” for more examples), in which a user should specify JAVA options, general parameters, problem instance, and solver instance:

$ cd myprojects
$ java -cp ../binary/MAOS_BIN.jar maosKernel.MAOSExecuter QAP:Problem=jeu_100_025_01 N=500 T=500 DUP_TIMES=10 solver=STD_NLDUX

//java: the JAVA executor, JAVA Runtime Environment Version 1.5 or above is preferred
//maosKernel.MAOSExecuter: the main execution entrance of the MAOS program

JAVA Options (See “java -help” for more information):

There is one recommended optional parameter for java:
  -server: select the "server" VM, which is normally faster than the "client" VM

The "-cp" option is used for loading the binary file "../release/MAOS_BIN.jar".

General Parameters:

NAME         VALUE_type   Range      Default_Value   Description

QAP:Problem  String      *	     <Problem_Name>  The problem instance to be solved
--------------------------------------------------------------------------------------------------
N            integer     >1          100 	     The number of agents
T            integer     >0          500	     Terminate condition: The maximum learning cycles
Tcon         integer     >0          -1              Terminate condition: The number of cycles as the best state is unvaried
                                                     //If Tcon==-1, then Tcon=T

DUP_TIMES    integer     >0          2		     Number of trials
--------------------------------------------------------------------------------------------------
Solver       String      *	     <Solver_Name>   The name of the script of the actual solver

//The explanation of Problem_Name and Solver_Name can be found in Directories & Files.

Output Information

For the output, we provide screen output, output a file for the running result, and stored the best solution ever found.

Screen Output:

[Initialization information]: provide the parsing information during the initialization.
[Runtime information]: The program outputs runtime information, i.e., the current best evaluation values, execution time, at every "Tout" cycles.
[Summary information]: At the end, it outputs the input variables, response values, and evaluation values <Vcon, Vopt> of the best solution.

Result File:

The result file will be stored at the directory "myprojects/results".

Solution File:

The best solution (better than any previous solutions) will be stored at the directory "myprojects/tasks/QAP/solution" (of the QAPLIB format).

References

[1] Xiao-Feng Xie. Round-table group optimization for sequencing problems. International Journal of Applied Metaheuristic Computing, 3(4): 1-24, 2012.

@Article{Xie2012a,
Title = {Round-table group optimization for sequencing problems},
Author = {Xiao-Feng Xie},
Journal = {International Journal of Applied Metaheuristic Computing},
Year = {2012},
Number = {4},
Pages = {1-24},
PDF={http://www.wiomax.com/team/xie/paper/IJAMC12.pdf},
DOI={10.4018/jamc.2012100101},
Code={http://www.wiomax.com/maos-qap},
Volume = {3}
}

February 26, 2017
0

Ant Colony Optimization (ACO) Algorithms

Tags : aco cgo optimization tsp

Category : Research , Software

Ant colony optimization (ACO), or ant system (AS), is a class of metaheuristic optimization algorithms inspired by the emergent search behavior using pheromone trails in natural ants.

We present CGO-AS, a generalized ant system (AS) implemented in the framework of cooperative group optimization (CGO), to show the leveraged optimization with a mixed individual and social learning. Ant colony is a simple yet efficient natural system for understanding the effects of primary intelligence on optimization. However, existing AS algorithms are mostly focusing on their capability of using social heuristic cues while ignoring their individual learning. CGO can integrate the advantages of a cooperative group and a low-level algorithm portfolio design, and the agents of CGO can explore both individual and social search. In CGO-AS, each ant (agent) is added with an individual memory, and is implemented with a novel search strategy to use individual and social cues in a controlled proportion. The presented CGO-AS is therefore especially useful in exposing the power of the mixed individual and social learning for improving optimization. The optimization performance is tested with instances of the traveling salesman problem (TSP). The results prove that a cooperative ant group using both individual and social learning obtains a better performance than the systems solely using either individual or social learning. The best performance is achieved under the condition when agents use individual memory as their primary information source, and simultaneously use social memory as their searching guidance. In comparison with existing AS systems, CGO-AS retains a faster learning speed toward those higher-quality solutions, especially in the later learning cycles. The leverage in optimization by CGO-AS is highly possible due to its inherent feature of adaptively maintaining the population diversity in the individual memory of agents, and of accelerating the learning process with accumulated knowledge in the social memory.

Xiao-Feng Xie and Zun-Jing Wang. Cooperative group optimization with ants (CGO-AS): Leverage optimization with mixed individual and social learning. Applied Soft Computing, 50: 223-234, 2017.

@Article{Xie2017Ants,
Title = {Cooperative group optimization with ants (CGO-AS): Leverage optimization with mixed individual and social learning},
Author = {Xiao-Feng Xie and Zun-Jing Wang},
Journal = {Applied Soft Computing},
Year = {2017},
Pages = {223--234},
Doi = {10.1016/j.asoc.2016.11.018},
PDF={http://www.wiomax.com/team/xie/paper/ASOC17.pdf},
Volume = {50}
}

January 23, 2017
0

Cooperative Group Optimization System (CGO)

Tags : optimization software

Category : Projects

The cooperative group optimization (CGO) system consists of a group of intelligent agents cooperating with their peers in a sharing environment for realizing a common intention of finding high-quality solution(s) based on the landscape representation of an optimization task.

Numerical Optimization

CGO has also been applied on numerical optimization problem (NOP) to find solutions in high-dimensional nonlinear continuous space. Some algorithms, including Dissipative Particle Swarm Optimization (DPSO), Differential Evolution (DE), Social Cognitive Optimization (SCO), Genetic Algorithms (GA), and Electromagnetism-like Mechanism (EM) Heuristic, etc, and their hybrids (e.g., DEPSO), could be easily implemented into CGO.

Both SCO and DEPSO have been incorporated into the NLPSolver extension of Calc in Apache Office. DEPSO was used for finding narrow admissible k-tuples.

Xiao-Feng Xie, Jiming Liu, and Zun-Jing Wang. A cooperative group optimization system. Soft Computing, 18(3): 469-495, 2014.

@Article{xie2014cooperative,
Title = {A cooperative group optimization system},
Author = {Xie, Xiao-Feng and Liu, Jiming and Wang, Zun-Jing},
Journal = {Soft Computing},
Year = {2014},
Number = {3},
Pages = {469--495},
Volume = {18},
PDF={http://www.wiomax.com/team/xie/paper/SOCO14.pdf},
DOI={10.1007/s00500-013-1069-8},
Publisher = {Springer}
}

Xiao-Feng Xie and Jiming Liu. A compact multiagent system based on autonomy oriented computing. In IEEE/WIC/ACM International Conference on Intelligent Agent Technology (IAT), pages 38-44, Compiegne, France, 2005. IEEE.

@InProceedings{Xie:2005p1406,
Title = {A compact multiagent system based on autonomy oriented computing},
Author = {Xiao-Feng Xie and Jiming Liu},
Booktitle = {IEEE/WIC/ACM International Conference on Intelligent Agent Technology (IAT)},
Address = {Compiegne, France},
Year = {2005},
PDF={http://www.wiomax.com/team/xie/paper/IAT05.pdf},
DOI={10.1109/IAT.2005.6},
Pages = {38--44},
Publisher = {IEEE}
}

Xiao-Feng Xie and Wen-Jun Zhang. SWAF: Swarm algorithm framework for numerical optimization. In Genetic and Evolutionary Computation Conference (GECCO), pages 238-250, Seattle, WA, USA, 2004. Springer.

@InProceedings{Xie:2004p238,
Title = {{SWAF}: Swarm algorithm framework for numerical optimization},
Author = {Xiao-Feng Xie and Wen-Jun Zhang},
Booktitle = {Genetic and Evolutionary Computation Conference (GECCO)},
Year = {2004},
PDF={http://www.wiomax.com/team/xie/paper/GECCO04_SWAF.pdf},
DOI={10.1007/978-3-540-24854-5_21},
Address = {Seattle, WA, USA},
Pages = {238--250},
Publisher = {Springer}
}

Xiao-Feng Xie and Wen-Jun Zhang. Solving engineering design problems by social cognitive optimization. In Genetic and Evolutionary Computation Conference (GECCO), pages 261-262, Seattle, WA, USA, 2004.

@InProceedings{Xie:2004p261,
Title = {Solving engineering design problems by social cognitive optimization},
Author = {Xiao-Feng Xie and Wen-Jun Zhang},
Booktitle = {Genetic and Evolutionary Computation Conference (GECCO)},
Year = {2004},
Pages = {261--262},
PDF={http://www.wiomax.com/team/xie/paper/GECCO04_SCO.pdf},
DOI={10.1007/978-3-540-24854-5_27},
Code={http://www.wiomax.com/sco},
Address = {Seattle, WA, USA}
}

Xiao-Feng Xie, Wen-Jun Zhang, and De-Chun Bi. Optimizing semiconductor devices by self-organizing particle swarm. In Congress on Evolutionary Computation (CEC), pages 2017-2022, Portland, OR, USA, 2004.

@InProceedings{Xie:2004p2017,
Title = {Optimizing semiconductor devices by self-organizing particle swarm},
Author = {Xiao-Feng Xie and Wen-Jun Zhang and De-Chun Bi},
Year = {2004},
Pages = {2017--2022},
Booktitle = {Congress on Evolutionary Computation (CEC)},
PDF={http://www.wiomax.com/team/xie/paper/CEC04_SOPSO.pdf},
DOI={10.1109/CEC.2004.1331144},
Address = {Portland, OR, USA}
}

Wen-Jun Zhang, Xiao-Feng Xie, and De-Chun Bi. Handling boundary constraints for numerical optimization by particle swarm flying in periodic search space. In Congress on Evolutionary Computation (CEC), pages 2307-2311, Portland, OR, USA, 2004.

@InProceedings{Zhang:2004p2307,
Title = {Handling boundary constraints for numerical optimization by particle swarm flying in periodic search space},
Author = {Wen-Jun Zhang and Xiao-Feng Xie and De-Chun Bi},
Year = {2004},
Pages = {2307-2311},
Booktitle = {Congress on Evolutionary Computation (CEC)},
PDF={http://www.wiomax.com/team/xie/paper/CEC04_PBR.pdf},
DOI={10.1109/CEC.2004.1331185},
Address = {Portland, OR, USA}
}

Xiao-Feng Xie, Wen-Jun Zhang, Guo-Rui Zhang, and Zhi-Lian Yang. Empirical study of differential evolution. Control and Decision, 19(1): 49-52, 2004.

@article{xie2004empirical,
title={Empirical study of differential evolution},
author={Xiao-Feng Xie and Wen-Jun Zhang and Guo-Rui Zhang and Zhi-Lian Yang},
journal={Control and Decision},
volume={19},
Number= {1},
pages={49--52},
year={2004}
}

Wen-Jun Zhang and Xiao-Feng Xie. DEPSO: Hybrid particle swarm with differential evolution operator. In IEEE International Conference on Systems, Man, and Cybernetics, pages 3816-3821, Washington, DC, USA, 2003. IEEE.

@InProceedings{Zhang:2003p3816,
Title = {{DEPSO}: Hybrid particle swarm with differential evolution operator},
Author = {Wen-Jun Zhang and Xiao-Feng Xie},
Booktitle = {IEEE International Conference on Systems, Man, and Cybernetics},
Year = {2003},
PDF={http://www.wiomax.com/team/xie/paper/SMCC03.pdf},
DOI={10.1109/ICSMC.2003.1244483},
Code={http://www.wiomax.com/depso},
Address = {Washington, DC, USA},
Pages = {3816--3821},
Publisher = {IEEE}
}

Xiao-Feng Xie, Wen-Jun Zhang, Jun Ruan, and Zhi-Lian Yang. Simulation optimization with multiple-demes genetic algorithms in master-slave parallel mode. Chinese Journal of Electronics, 12(2): 254-258, 2003.

@article{xie2003simulation,
title={Simulation optimization with multiple-demes genetic algorithms in master-slave parallel mode},
author={Xiao-Feng Xie and Wen-Jun Zhang and Jun Ruan and Zhi-Lian Yang},
journal={Chinese Journal of Electronics},
volume={12},
Number= {2},
pages={254--258},
PDF={http://www.wiomax.com/team/xie/paper/DZXB03.pdf},
year={2003}
}

Xiao-Feng Xie, Wen-Jun Zhang, and Zhi-Lian Yang. Overview of particle swarm optimization. Control and Decision, 18(2): 129-134, 2003.

@article{xie2003overview,
title={Overview of particle swarm optimization},
author={Xiao-Feng Xie and Wen-Jun Zhang and Zhi-Lian Yang},
journal={Control and Decision},
volume={18},
Number= {2},
pages={129--134},
year={2003}
}

Xiao-Feng Xie, Wen-Jun Zhang, and Zhi-Lian Yang. Social cognitive optimization for nonlinear programming problems. In International Conference on Machine Learning and Cybernetics (ICMLC), pages 779-783, Beijing, China, 2002.

@InProceedings{Xie:2002p779,
Title = {Social cognitive optimization for nonlinear programming problems},
Author = {Xiao-Feng Xie and Wen-Jun Zhang and Zhi-Lian Yang},
Booktitle = {International Conference on Machine Learning and Cybernetics (ICMLC)},
Year = {2002},
PDF={http://www.wiomax.com/team/xie/paper/ICMLC02A.pdf},
DOI={10.1109/ICMLC.2002.1174487},
Code={http://www.wiomax.com/sco},
Address = {Beijing, China},
Pages = {779--783}
}

Xiao-Feng Xie, Wen-Jun Zhang, and Zhi-Lian Yang. A dissipative particle swarm optimization. In Congress on Evolutionary Computation (CEC), pages 1456-1461, Honolulu, HI, USA, 2002.

@InProceedings{Xie:2002p1456,
Title = {A dissipative particle swarm optimization},
Author = {Xiao-Feng Xie and Wen-Jun Zhang and Zhi-Lian Yang},
Booktitle = {Congress on Evolutionary Computation (CEC)},
Year = {2002},
Address = {Honolulu, HI, USA},
PDF={http://www.wiomax.com/team/xie/paper/CEC02.pdf},
DOI={10.1109/CEC.2002.1004457},
Code={http://www.wiomax.com/dpso},
Pages = {1456--1461}
}

Xiao-Feng Xie, Wen-Jun Zhang, and Zhi-Lian Yang. Adaptive particle swarm optimization on individual level. In International Conference on Signal Processing (ICSP), pages 1215-1218, Beijing, China, 2002.

@InProceedings{Xie:2002p1215,
Title = {Adaptive particle swarm optimization on individual level},
Author = {Xiao-Feng Xie and Wen-Jun Zhang and Zhi-Lian Yang},
Booktitle = {International Conference on Signal Processing (ICSP)},
Year = {2002},
Address = {Beijing, China},
PDF={http://www.wiomax.com/team/xie/paper/ICSP02.pdf},
DOI={http://dx.doi.org/10.1109/ICOSP.2002.1180009},
Pages = {1215--1218}
}

Xiao-Feng Xie, Wen-Jun Zhang, and Zhi-Lian Yang. Hybrid particle swarm optimizer with mass extinction. In International Conference on Communication, Circuits and Systems (ICCCAS), pages 1170-1173, Chengdu, China, 2002.

@InProceedings{Xie:2002p1170,
Title = {Hybrid particle swarm optimizer with mass extinction},
Author = {Xiao-Feng Xie and Wen-Jun Zhang and Zhi-Lian Yang},
Booktitle = {International Conference on Communication, Circuits and Systems (ICCCAS)},
Year = {2002},
Address = {Chengdu, China},
PDF={http://www.wiomax.com/team/xie/paper/ICCCAS02.pdf},
DOI={http://dx.doi.org/10.1109/ICCCAS.2002.1178992},
Pages = {1170-1173}
}

Xiao-Feng Xie, Wen-Jun Zhang, and Zhi-Lian Yang. Solving numerical optimization problems by simulating particle-wave duality and social information sharing. In International Conference on Artificial Intelligence (IC-AI), pages 1163-1169, Las Vegas, NE, USA, 2002.

@InProceedings{Xie:2002p1163,
Title = {Solving numerical optimization problems by simulating particle-wave duality and social information sharing},
Author = {Xiao-Feng Xie and Wen-Jun Zhang and Zhi-Lian Yang},
Booktitle = {International Conference on Artificial Intelligence (IC-AI)},
Year = {2002},
Address = {Las Vegas, NE, USA},
PDF={http://www.wiomax.com/team/xie/paper/ICAI02.pdf},
Pages = {1163-1169}
}

Xiao-Feng Xie, Wen-Jun Zhang, and Zhi-Lian Yang. A parents selection strategy fighting premature convergence in floating genetic algorithms. Control and Decision, 17(5): 625-628, 2002.

@article{xie2002parents,
title={A parents selection strategy fighting premature convergence in floating genetic algorithms},
author={Xiao-Feng Xie and Wen-Jun Zhang and Zhi-Lian Yang},
journal={Control and Decision},
volume={17},
Number = {5},
pages={625--628},
year={2002}
}

Combinatorial Optimization

CGO can also been applied on some combinatorial optimization problems, such as Travelling Salesman Problem (TSP), Graph Coloring Problem (GCP), Quadratic Knapsack Problem (QKP), Flow-Shop Scheduling Problem (FSP), Quadratic Assignment Problem (QAP), etc, by combining with low-level Metaheuristic Local Search techniques.

Xiao-Feng Xie and Zun-Jing Wang. Cooperative group optimization with ants (CGO-AS): Leverage optimization with mixed individual and social learning. Applied Soft Computing, 50: 223-234, 2017.

@Article{Xie2017Ants,
Title = {Cooperative group optimization with ants (CGO-AS): Leverage optimization with mixed individual and social learning},
Author = {Xiao-Feng Xie and Zun-Jing Wang},
Journal = {Applied Soft Computing},
Year = {2017},
Pages = {223--234},
Doi = {10.1016/j.asoc.2016.11.018},
PDF={http://www.wiomax.com/team/xie/paper/ASOC17.pdf},
Volume = {50}
}

Xiao-Feng Xie. Round-table group optimization for sequencing problems. International Journal of Applied Metaheuristic Computing, 3(4): 1-24, 2012.

@Article{Xie2012a,
Title = {Round-table group optimization for sequencing problems},
Author = {Xiao-Feng Xie},
Journal = {International Journal of Applied Metaheuristic Computing},
Year = {2012},
Number = {4},
Pages = {1-24},
PDF={http://www.wiomax.com/team/xie/paper/IJAMC12.pdf},
DOI={10.4018/jamc.2012100101},
Code={http://www.wiomax.com/maos-qap},
Volume = {3}
}

Xiao-Feng Xie and Jiming Liu. Multiagent optimization system for solving the traveling salesman problem (TSP). IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 39(2): 489-502, 2009.

@Article{xie2009multiagent,
Title = {Multiagent optimization system for solving the traveling salesman problem ({TSP})},
Author = {Xiao-Feng Xie and Jiming Liu},
Journal = {IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics},
Year = {2009},
Number = {2},
Pages = {489--502},
PDF={http://www.wiomax.com/team/xie/paper/TSMCB09.pdf},
DOI={10.1109/TSMCB.2008.2006910},
Code={http://www.wiomax.com/maos-tsp},
Volume = {39}
}

Xiao-Feng Xie and Jiming Liu. Graph coloring by multiagent fusion search. Journal of Combinatorial Optimization, 18(2): 99-123, 2009.

@Article{xie2009graph,
Title = {Graph coloring by multiagent fusion search},
Author = {Xiao-Feng Xie and Jiming Liu},
Journal = {Journal of Combinatorial Optimization},
Year = {2009},
Number = {2},
Pages = {99--123},
PDF={http://www.wiomax.com/team/xie/paper/JOCO09.pdf},
DOI={10.1007/s10878-008-9140-6},
Code={http://www.wiomax.com/maos-gcp},
Volume = {18}
}

Xiao-Feng Xie and Jiming Liu. A mini-swarm for the quadratic knapsack problem. In IEEE Swarm Intelligence Symposium, pages 190-197, Honolulu, HI, USA, 2007.

@InProceedings{Xie:2007p190,
Title = {A mini-swarm for the quadratic knapsack problem},
Author = {Xiao-Feng Xie and Jiming Liu},
Year = {2007},
Pages = {190--197},
Address = {Honolulu, HI, USA},
PDF={http://www.wiomax.com/team/xie/paper/SIS07.pdf},
DOI={10.1109/SIS.2007.368045},
Code={http://www.wiomax.com/maos-qkp},
Booktitle = {IEEE Swarm Intelligence Symposium}
}

Xiao-Feng Xie and Jiming Liu. How autonomy oriented computing (AOC) tackles a computationally hard optimization problems. In International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS), pages 646-653, Hakodate, Japan, 2006.

@InProceedings{Xie:2006p646,
Title = {How autonomy oriented computing ({AOC}) tackles a computationally hard optimization problems},
Author = {Xiao-Feng Xie and Jiming Liu},
Year = {2006},
Pages = {646--653},
PDF={http://www.wiomax.com/team/xie/paper/AAMAS06.pdf},
DOI={10.1145/1160633.1160747},
Address = {Hakodate, Japan},
Booktitle = {International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS)}
}

August 13, 2016
0

Smart and Scalable Urban Signal Networks

Tags : artificial intelligence smart cities transportation

Category : Projects

This system is a real-time adaptive traffic control system, which combines artificial intelligence (AI) and traffic theory to optimize highly dynamic traffic flow in urban road networks. The system (smart, adaptable traffic signals) is listed as 25 Great Things about Computer Science at Carnegie Mellon.

Xiao-Feng Xie, et al. Smart and Scalable Urban Signal Networks: Methods and Systems for Adaptive Traffic Signal Control. U.S. Patent No. 9,159,229, 2015.

As the lead inventor of the system, Dr. Xie has created its core control engine, which combines schedule-driven intersection control (SchIC) with decentralized coordination mechanisms (in the sense of Internet of Smart Intersections, an instance of Smart IoT). He has also designed and realized the strengthening strategies to enable the real-world operations of the system in the field.

➥ Please visit here for our recent transportation research and studies on smart mobility and road safety beyond this work. Examples include:

X. Xie and Z. Wang, “Combined traffic control and route choice optimization for traffic networks with disruptive changes,” Transportmetrica B: Transport Dynamics, vol. 7, iss. 1, pp. 814-833, 2019.

@Article{Xie2018RCTC2,
Title = {Combined traffic control and route choice optimization for traffic networks with disruptive changes},
Author = {Xiao-Feng Xie and Zun-Jing Wang},
Journal = {Transportmetrica B: Transport Dynamics},
Volume = {7},
number={1},
Pages = {814-833},
Doi = {10.1080/21680566.2018.1517059},
Year = {2019}
}

X. Xie and Z. Wang, “Examining travel patterns and characteristics in a bikesharing network and implications for data-driven decision supports: Case study in the Washington DC area,” Journal of Transport Geography, vol. 71, pp. 84-102, 2018.

@Article{Xie2018Bike,
Title = {Examining travel patterns and characteristics in a bikesharing network and implications for data-driven decision supports: Case study in the {Washington DC} area},
Author = {Xiao-Feng Xie and Zun-Jing Wang},
Journal = {Journal of Transport Geography},
Volume = {71},
Pages = {84--102},
PDF={http://www.wiomax.com/team/xie/paper/JTRG18Pre.pdf},
Doi = {10.1016/j.jtrangeo.2018.07.010},
Year = {2018}
}

X. Xie and Z. Wang, “SIV-DSS: Smart in-vehicle decision support system for driving at signalized intersections with V2I communication,” Transportation Research Part C, vol. 90, pp. 181-197, 2018.

@Article{Xie2018SIV,
Title = {{SIV-DSS}: Smart in-vehicle decision support system for driving at signalized intersections with {V2I} communication},
Author = {Xiao-Feng Xie and Zun-Jing Wang},
Journal = {Transportation Research Part C},
Volume = {90},
Pages = {181--197},
PDF={http://www.wiomax.com/team/xie/paper/TRC18Pre.pdf},
Doi = {10.1016/j.trc.2018.03.008},
Year = {2018}
}

X. Xie and Z. Wang, “Multiscale crash analysis: A case study of integrating FARS, Maryland’s crash data, and Montgomery County’s traffic violation data,” in Transportation Research Board (TRB) Annual Meeting, Washington, DC, 2018.

@InProceedings{xie2018multiscale,
title={Multiscale crash analysis: A case study of integrating {FARS}, {Maryland}'s crash data, and {Montgomery County}'s traffic violation data},
author={Xie, Xiao-Feng and Wang, Zun-Jing},
Booktitle = {Transportation Research Board (TRB) Annual Meeting},
number={18-2283},
Address = {Washington, DC},
LNK={https://trid.trb.org/View/1495254},
PDF={http://www.wiomax.com/team/xie/paper/TRB18.pdf},
year={2018}
}

Real-World Deployments

– (East Liberty) Deployed the the initial smart traffic lights for a network with nine intersections in the East Liberty neighborhood, Pittsburgh, PA. The system has been running since June 2012. Improvements of over 25% reductions in travel times, over 40% reductions in idle time, and a projected reduction in emissions of over 21% were achieved.

– (Bakery Square) Expanded the intelligent traffic signal control system further to include nine more intersections in the Bakery Square neighborhood, Pittsburgh, PA. The expanded system has been running since Oct 2013. Improvements of over 24% reductions in travel times, over 41% reductions in idle time, and a projected reduction in emissions of over 20% were achieved.

Publications

Xiao-Feng Xie, S. Smith, G. Barlow, and Ting-Wei Chen. Coping with real-world challenges in real-time urban traffic control. In Transportation Research Board (TRB) Annual Meeting, number 14-2103, Washington, DC, 2014.

@InProceedings{Xie2014a,
Title = {Coping with real-world challenges in real-time urban traffic control},
Author = {Xiao-Feng Xie and S. Smith and G. Barlow and Ting-Wei Chen},
Booktitle = {Transportation Research Board (TRB) Annual Meeting},
Year = {2014},
number={14-2103},
PDF={http://www.wiomax.com/team/xie/paper/TRB14UTC.pdf},
PPT={http://www.wiomax.com/team/xie/demo/TRB14_demo_Surtrac_Uncertainty.pdf},
LNK={https://trid.trb.org/View/1288134},
Address = {Washington, DC}
}

Xiao-Feng Xie, S. Smith, Ting-Wei Chen, and G. Barlow. Real-time traffic control for sustainable urban living. In IEEE International Conference on Intelligent Transportation Systems, pages 1863-1868, Qingdao, China, 2014.

@InProceedings{Xie2014ITSC,
Title = {Real-time traffic control for sustainable urban living},
Author = {Xiao-Feng Xie and S. Smith and Ting-Wei Chen and G. Barlow},
Booktitle = {IEEE International Conference on Intelligent Transportation Systems},
Address = {Qingdao, China},
Year = {2014},
PDF = {http://www.wiomax.com/team/xie/paper/ITSC14.pdf},
PPT={http://www.wiomax.com/team/xie/demo/ITSC14_demo_MMTC.pdf},
VID={https://www.youtube.com/watch?v=UBu6QtNiJVY},
DOI={10.1109/ITSC.2014.6957964},
Pages = {1863-1868}
}

Xiao-Feng Xie, S. Smith, Liang Lu, and G. Barlow. Schedule-driven intersection control. Transportation Research Part C, 24: 168-189, 2012.

@Article{Xie2012,
Title = {Schedule-driven intersection control},
Author = {Xiao-Feng Xie and S. Smith and Liang Lu and G. Barlow},
Journal = {Transportation Research Part C},
Year = {2012},
Pages = {168-189},
Volume = {24},
PDF={http://www.wiomax.com/team/xie/paper/TRC12.pdf},
Doi = {10.1016/j.trc.2012.03.004}
}

Xiao-Feng Xie, S. Smith, and G. Barlow. Schedule-driven coordination for real-time traffic network control. In International Conference on Automated Planning and Scheduling (ICAPS), pages 323-331, Sao Paulo, Brazil, 2012.

@InProceedings{Xie2012c,
Title = {Schedule-driven coordination for real-time traffic network control},
Author = {Xiao-Feng Xie and S. Smith and G. Barlow},
Booktitle = {{International Conference on Automated Planning and Scheduling (ICAPS)}},
Year = {2012},
PDF={http://www.wiomax.com/team/xie/paper/ICAPS12.pdf},
VID={https://www.youtube.com/watch?v=d_BCzByquGg},
Address = {Sao Paulo, Brazil},
Pages = {323--331}
}

Xiao-Feng Xie, S. Smith, and G. Barlow. Coordinated look-ahead scheduling for real-time traffic signal control. In International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS), pages 1271-1272, Valencia, Spain, 2012.

@InProceedings{Xie2012b,
Title = {Coordinated look-ahead scheduling for real-time traffic signal control},
Author = {Xiao-Feng Xie and S. Smith and G. Barlow},
Booktitle = {{International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS)}},
Year = {2012},
Address = {Valencia, Spain},
PDF={http://www.wiomax.com/team/xie/paper/AAMAS12.pdf},
PPT={http://www.wiomax.com/team/xie/demo/AAMAS12_demo_Surtrac.pdf},
LNK={http://dl.acm.org/citation.cfm?id=2343958},
Pages = {1271-1272}
}

Xiao-Feng Xie, G. Barlow, S. Smith, and Z. Rubinstein. Platoon-based self-scheduling for real-time traffic signal control. In IEEE International Conference on Intelligent Transportation Systems, pages 879-884, Washington, DC, USA, 2011.

@InProceedings{Xie2011,
Title = {Platoon-based self-scheduling for real-time traffic signal control},
Author = {Xiao-Feng Xie and G. Barlow and S. Smith and Z. Rubinstein},
Booktitle = {IEEE International Conference on Intelligent Transportation Systems},
Year = {2011},
PDF={http://www.wiomax.com/team/xie/paper/ITSC11.pdf},
VID={https://www.youtube.com/watch?v=gkDsgMG1eg0},
DOI={10.1109/ITSC.2011.6082849},
Address = {Washington, DC, USA},
Pages = {879--884}
}

– This work was supported in part by the Robotics Institute of CMU, with support from the Hillman Foundation, the Heinz Endowments, and the R. K. Mellon Foundation.

Xiao-Feng Xie, Ph.D.

Category Archives: Projects

0

Work on Big Data Analytics and Urban Computing

0

(Constrained) Numerical Optimization Problem (NOP)

0

MAOS-TSP: Project Portal

0

MAOS-GCP: Project Portal

0

MAOS-QKP: Project Portal

0

MAOS-FSP: Project Portal

0

MAOS-QAP: Project Portal

0

Ant Colony Optimization (ACO) Algorithms

0

Cooperative Group Optimization System (CGO)

0

Smart and Scalable Urban Signal Networks

Archives