MAOS-TSP: Project Portal
Category : Open Source
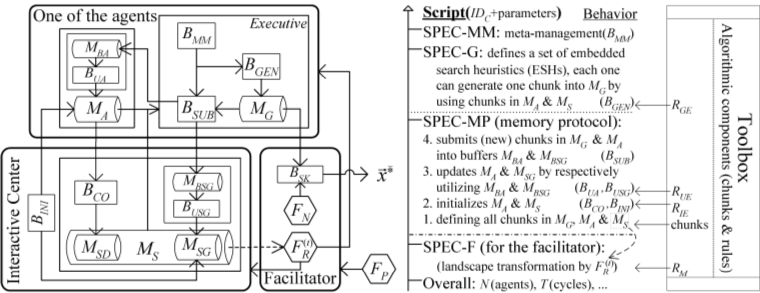
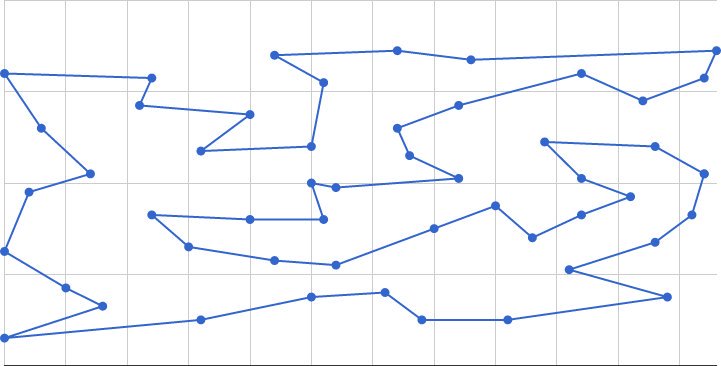
 MAOS-TSP [1] is a multiagent optimization system (MAOS) for solving the Traveling Salesman Problem (TSP).
MAOS-TSP [1] is a multiagent optimization system (MAOS) for solving the Traveling Salesman Problem (TSP).
Related Information: Please find other related code and software in our Source Code Library.
| Basic Description | What’s New | Directories & Files | Command Line & Parameters | Output Information | References | Contact |
|---|
License Information: You can redistribute and/or modify it under the terms of the Creative Commons Non-Commercial License 3.0.
System Requirements: MAOS-TSP is a platform-independent software developed by JAVA version 1.5 or above.
|
What’s New
|
|---|
Version V1.0.004 [Download | github]:
– Add a parameter “opt=[length]” to use the length of the shortest tour as another stopping criterion. (Based on the request by J. Bossek)
Version V1.0.003:
– Solver “STD_PRB_3Opt_2L_REAX+SEAX_1J”: 1) Two-level representation for 3-opt: reduce the time complexity of Tour Segment Inversion from O(n) to O(sqrt(n)); 2) Locking common edges during the sub-cycles bridging process in the generalized EAX; 3) Sorting in k Nearest Neighbors: reduce the time complexity from O(nlog(n)) to O(n+klog(k)).
Version V1.0.002:
– Solver “STD_PRB_3Opt_REAX+SEAX”: It implements the solver for original MAOS-TSP algorithm [1]. This solver has shown to be competitive in solving middle-scale TSP instances (1000 – 6000 nodes) as comparing to some state-of-the-art algorithms, without using explicit local search (e.g. LK variants) during the runtime cycles.
For example, it found the best-so-far solution (located in myprojects/tasks/TSP/solution) for the open instance fdp3256 in the VLSI Data Sets.
– Setting parameters: TSP:Problem, N, T, Tcon, Solver.
|
Directories & Files
|
|---|
binary // the binary code of MAOS-TSP
source // the source code of MAOS-TSP
myprojects // user directory
|-----> examples.bat // commandline examples
|-----> results // the directory for storing runtime results
|-----> setting // the setting directory
|-----> kernel // the setting directory for MAOS Kernel
|-----> TSP // the setting directory for TSP solvers
|-----> solver // the directory containing solver script files (the name of each file is Solver_Name)
// Examples: "STD_PRB_3Opt_REAX+SEAX" and "STD_PRB_3Opt_2L_REAX+SEAX_1J"
|-----> tasks // task directory
|-----> TSP
|-----> instance // GCP instances of the TSPLIB format (Problem_Name with the default suffix .tsp)
// Example: rl1323.tsp (Problem_Name is rl1323)
|-----> solution // the directory for storing solutions of TSP instances
// For a normal solution, the file name is Problem_Name.(objective value).tour
// If objective value is removed from the file name, the solution is considered as optimal.
// Example: fdp3256.tour
// Typical benchmark instances can be found in the TSPLIB and VLSI data sets.
|
Command Line & Parameters
|
|---|
MAOS-TSP is executed on the command line (Enter the directory “myprojects”, and execute maosKernel.MAOSExecuter). Here is a typical example (See the file “myprojects/Examples.bat” for more examples), in which a user should specify JAVA options, general parameters, problem instance, and solver instance:
$ cd myprojects $ java -server -Xmx512M -cp ../binary/MAOS_SEQ.jar maosKernel.MAOSExecuter TSP:Problem=rl1323 N=300 T=500 Tcon=100 DUP_TIMES=5 solver=STD_PRB_3Opt_2L_REAX+SEAX_1J //java: the JAVA executor, JAVA Runtime Environment Version 1.5 or above is preferred //maosKernel.MAOSExecuter: the main execution entrance of the MAOS program
JAVA Options (See “java -help” for more information):
There are two recommended optional parameters for java: -server: select the "server" VM, which is normally faster than the "client" VM -Xmx: set maximum Java heap size. Using a large enough size may prevent from the "out of memory" error Moreover, the "-cp" option is used for loading the binary file "../binary/MAOS_SEQ.jar".
General Parameters:
NAME VALUE_type Range Default_Value Description TSP:Problem String * <Problem_Name> The problem instance to be solved -------------------------------------------------------------------------------------------------- N integer >1 300 The number of agents T integer >0 500 Terminate condition: The maximum learning cycles Tcon integer >0 100 Terminate condition: The number of cycles as the best state is unvaried DUP_TIMES integer >0 10 Number of trials -------------------------------------------------------------------------------------------------- Solver String * <Solver_Name> The name of the script of the actual solver -------------------------------------------------------------------------------------------------- opt integer >0 None The lower bound tour length for termination
//The explanation of Problem_Name and Solver_Name can be found in Directories & Files.
|
Output Information
|
|---|
For the output, we provide screen output, output a file for the running result, and stored the best solution ever found.
Screen Output:
[Initialization information]: provide the parsing information during the initialization. [Runtime information]: The program outputs runtime information, i.e., the current best evaluation values, execution time, at every "Tout" cycles. [Summary information]: At the end, it outputs the input variables, response values, and evaluation values <Vcon, Vopt> of the best solution.
Result File:
The result file will be stored at the directory "myprojects/results".
Solution File:
The best solution (better than any previous solutions) will be stored at the directory "myprojects/tasks/TSP/solution" (of the TSPLIB format).
|
References
|
|---|
@Article{xie2009multiagent,
Title = {Multiagent optimization system for solving the traveling salesman problem ({TSP})},
Author = {Xiao-Feng Xie and Jiming Liu},
Journal = {IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics},
Year = {2009},
Number = {2},
Pages = {489--502},
PDF={http://www.wiomax.com/team/xie/paper/TSMCB09.pdf},
DOI={10.1109/TSMCB.2008.2006910},
Code={http://www.wiomax.com/maos-tsp},
Volume = {39}
}