I. Monte Carlo (MC) Method
MC is a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. They are most useful when it is difficult or impossible to use other mathematical methods. Monte Carlo methods are powerful for simulating systems with many coupled degrees of freedom. See our work below as an example on using MC to solve complex and hard problems:
- Z.-J. Wang, D. Frenkel. Pore nucleation in mechanically stretched bilayer membranes. Journal of Chemical Physics, 2005, 123: 154701. [DOI]
II. Molecular dynamics (MD) Method
MD is a computer simulation of physical movements of atoms and molecules in the context of N-body simulation. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms. MD simulations permit the study of complex, dynamic processes. A molecular dynamics simulation requires the definition of a potential function, or a description of the terms by which the particles in the simulation will interact. For the systems which obey the ergodic hypothesis, an MD simulation can be used to determine macroscopic thermodynamic properties. MD has also been termed “statistical mechanics by numbers” and “Laplace’s vision of Newtonian mechanics” of predicting the future by animating nature’s forces and allowing insight into molecular motion on an atomic scale. See our work below as an example on how to use MD method:
Study on Bubble Nucleation
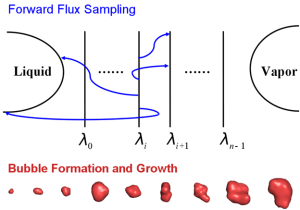 Bubble nucleation is difficult to study with traditional computational method. This is because, as a rare event, bubble nucleation is hard to happen due to the free-energy barrier; but once it happens, the process is fast. We incorporated the forward flux sampling (FFS) technique into molecular dynamics simulations, where the forward flux sampling allows us to track the pathways and flux of a rare phase transition between the liquid and the vapor of the phase space, while the molecular dynamics simulations allow us to study the kinetics of bubble nucleation process. This example shows how FFS-MD is powerful for studying kinetics, computing nucleation rate, and analyzing mechanism of bubble nucleation, a rare event.
Bubble nucleation is difficult to study with traditional computational method. This is because, as a rare event, bubble nucleation is hard to happen due to the free-energy barrier; but once it happens, the process is fast. We incorporated the forward flux sampling (FFS) technique into molecular dynamics simulations, where the forward flux sampling allows us to track the pathways and flux of a rare phase transition between the liquid and the vapor of the phase space, while the molecular dynamics simulations allow us to study the kinetics of bubble nucleation process. This example shows how FFS-MD is powerful for studying kinetics, computing nucleation rate, and analyzing mechanism of bubble nucleation, a rare event.
- Z.-J. Wang, C. Valeriani, D. Frenkel. Homogeneous bubble nucleation driven by local hot spots: a molecular dynamics study. Journal of Physical Chemistry B, 2009, 113(12): 3776-3784. [DOI]
Study on the Liquid-Vapor Interphase Transport
 Evaporation and condensation processes at the thin liquid-vapor interface may be investigated with MD combined with an efficient statistical method. The condensed then re-evaporated molecules can be successfully distinguished from the reflected molecules according to their different characteristic times. The kinetic characteristics of the condensed, reflected, and evaporated molecules can then be separately studied and compared. Here this example shows that MD is efficient in analyzing an interphase transport process from molecular level.
Evaporation and condensation processes at the thin liquid-vapor interface may be investigated with MD combined with an efficient statistical method. The condensed then re-evaporated molecules can be successfully distinguished from the reflected molecules according to their different characteristic times. The kinetic characteristics of the condensed, reflected, and evaporated molecules can then be separately studied and compared. Here this example shows that MD is efficient in analyzing an interphase transport process from molecular level.
- Z.-J. Wang, M. Chen, Z. Guo. A molecular study on the liquid-vapor interphase transport. Microscale Thermophysical Engineering, 2003, 7(4): 275-289.
- Z.-J. Wang, M. Chen, Z. Guo. Modified transition state theory for evaporation and condensation. Chinese Physics Letter, 2002, 19(4): 537-539.
Study of the Liquid-Vapor Interfacial Profiles
 MD is useful in studying the thermodynamic properties of liquid-vapor interfaces. The density profile, the temperature profile and the pressure tensor can all be obtained with MD. There exist a sharp peak and a small valley at the thin region outside the liquid-vapor interface in the local kinetic energy distribution across the interface. When the system temperature increases, the magnitude of the peak and the valley decreases. This non-equilibrium molecular kinetic energy distribution located at the thin region outside the liquid-vapor interface, indicating that although the liquid and vapor phases are in thermodynamic equilibrium, the interface may not be in thermostatic equilibrium. This is an example showing how to use MD to study a local non-equilibrium process at a ultra-thin interface or film.
MD is useful in studying the thermodynamic properties of liquid-vapor interfaces. The density profile, the temperature profile and the pressure tensor can all be obtained with MD. There exist a sharp peak and a small valley at the thin region outside the liquid-vapor interface in the local kinetic energy distribution across the interface. When the system temperature increases, the magnitude of the peak and the valley decreases. This non-equilibrium molecular kinetic energy distribution located at the thin region outside the liquid-vapor interface, indicating that although the liquid and vapor phases are in thermodynamic equilibrium, the interface may not be in thermostatic equilibrium. This is an example showing how to use MD to study a local non-equilibrium process at a ultra-thin interface or film.
- Z.-J. Wang, M. Chen, Z. Guo, C. Yang. Molecular dynamics study on the liquid-vapor interfacial profiles. Fluid Phase Equilibria, 2001, 183-184: 321-329.
